Month: January 2014

Categories
Book Notes Problems Variable Substitutions

Mathematical Quickies No.122

This problem kind of bugs me. Here is the problem and my first step:

Mathematical Quickies No.122

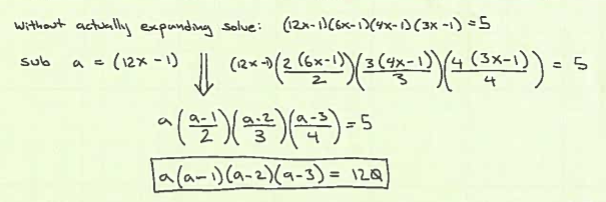
So I like my first step – but then my way of solving {a(a-1)(a-2)(a-3) = 120} is wonky. I want to expand it and use the quadratic equation – which is not slick enough to be what they are after. I am not seeing synthetic division, or any usual suspects – so I think I am missing something obvious.

Rick, someone I work with, looked at the problem and immediately said you could tell that the solution needed to be divisible by 5, which happens to be a valid solution here. However I don’t believe that is always the case though.

My way to get the solution shows a solution of {-2,5}. Work shown here.

Categories
Book Notes Problems Variable Substitutions

Mathematical Quickies No.84

This is another example of a substitution problem. Normally I would have just worked it out long hand, expanding thing and solving. That’s a lot of work and frankly kind of a foolish way to attack the problem looking at it now. Since I started looking for substitutions first – the problem collapses to simple in one substitution. Unfortunately its still fairly un-elegant – so I don’t think this is the solution they book is looking for.

The problem is stated as: “Solve: (6x+28)^1/3 – (6x-28)^1/3 = 2”

My solution

Categories
Algrebra Book Notes Problems

Mathematical Quickies No.205

I kind of hate problems where the solution is to find the most elegant answer possible. This problem is an excellent example of why. My solution (here), solves the problem as stated – but I took a grinder solution just wearing the problem away. My gut says that there is no way that this is the solution they want – however I do solve it with multiple applications of the quadratic equation, which the problem framing hinted at, so I am posting it for now.

Knowing that this is not the solution they wanted, I want to go look at the back of the book to confirm that is the case, and see what they were after. The problem with looking though is that I ruin the problem. So, I pretty much never want to look – hence my dislike of problems I where I can not prove I have the right solution. They all seem to be asking me to prove that someone smarter than I am could not solve the problem in a more elegant manner, but since the person in question is by definition smarter than I am – well – it seems a might ridiculous.

Here we have the problem:

“Solve this equation using nothing higher tan quadratic equations:

X = Sqrt( (X-(1/X)) + Sqrt(1-(1/X)) )”

My Solution

Categories
Math Puzzles Variable Substitutions

Mathematical Quickies No.226

So for some reason I never started looking for substitutions when solving equations. It was certainly something I learned to do when analyzing circuits, but when I see a math problem I never started looking for substitutions that might simplify the problem. Until recently.

Looking at, I think this problem, it “just clicked” – and I started looking for substitutions. Then used them to nock out answers for the next half dozen puzzle problems I tackled. Weird, since I am not doing anything I did not know before, but I just started looking at problems differently.

This one is fairly straight forward:

Solve: (x-a)/b + (x-b)/a = b/(x-a) + a/(x-b)

It becomes way easier to solve after a simple substitution.
My Solution.