Author: Aaron

Koei-Kan green belt test

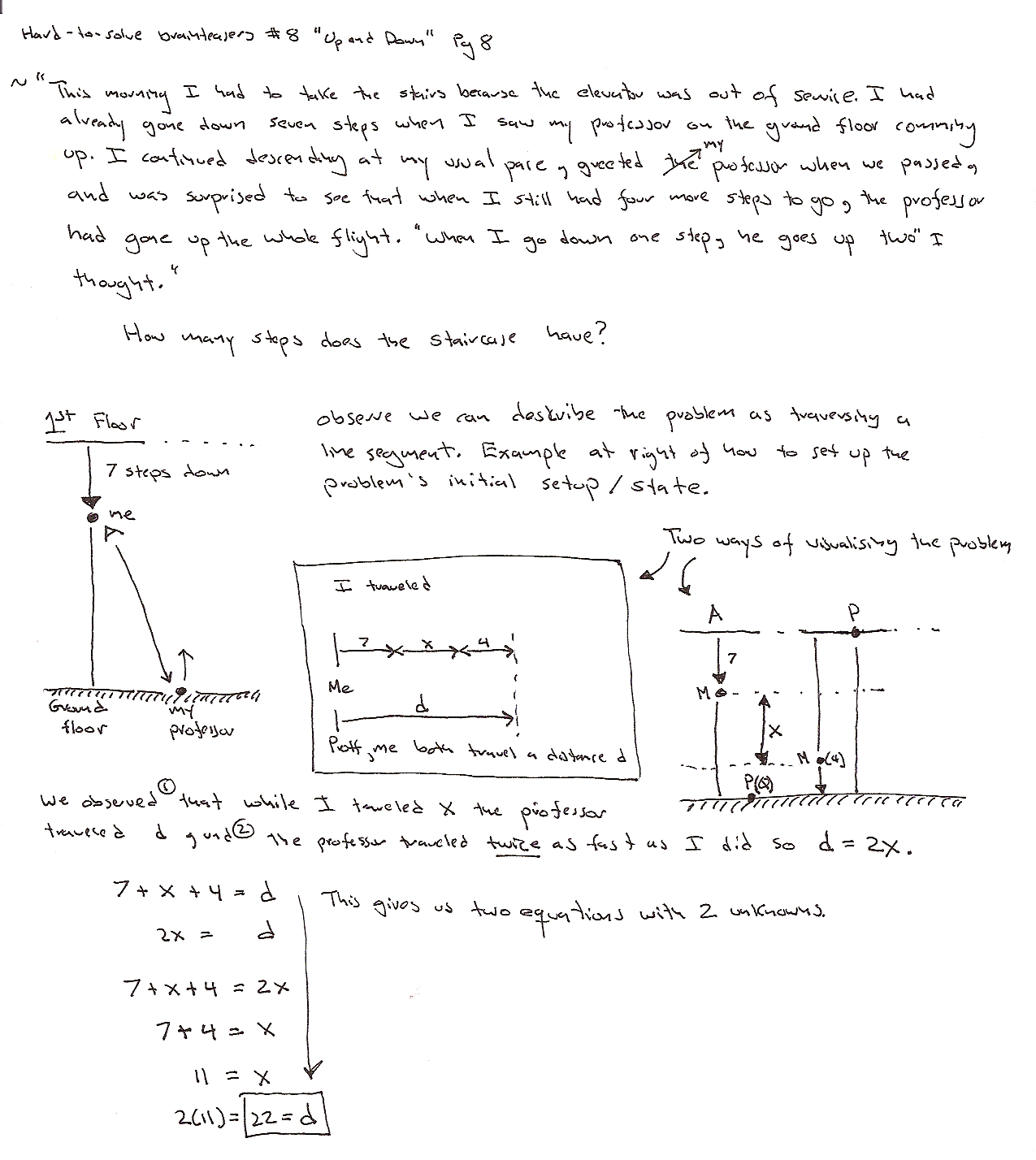
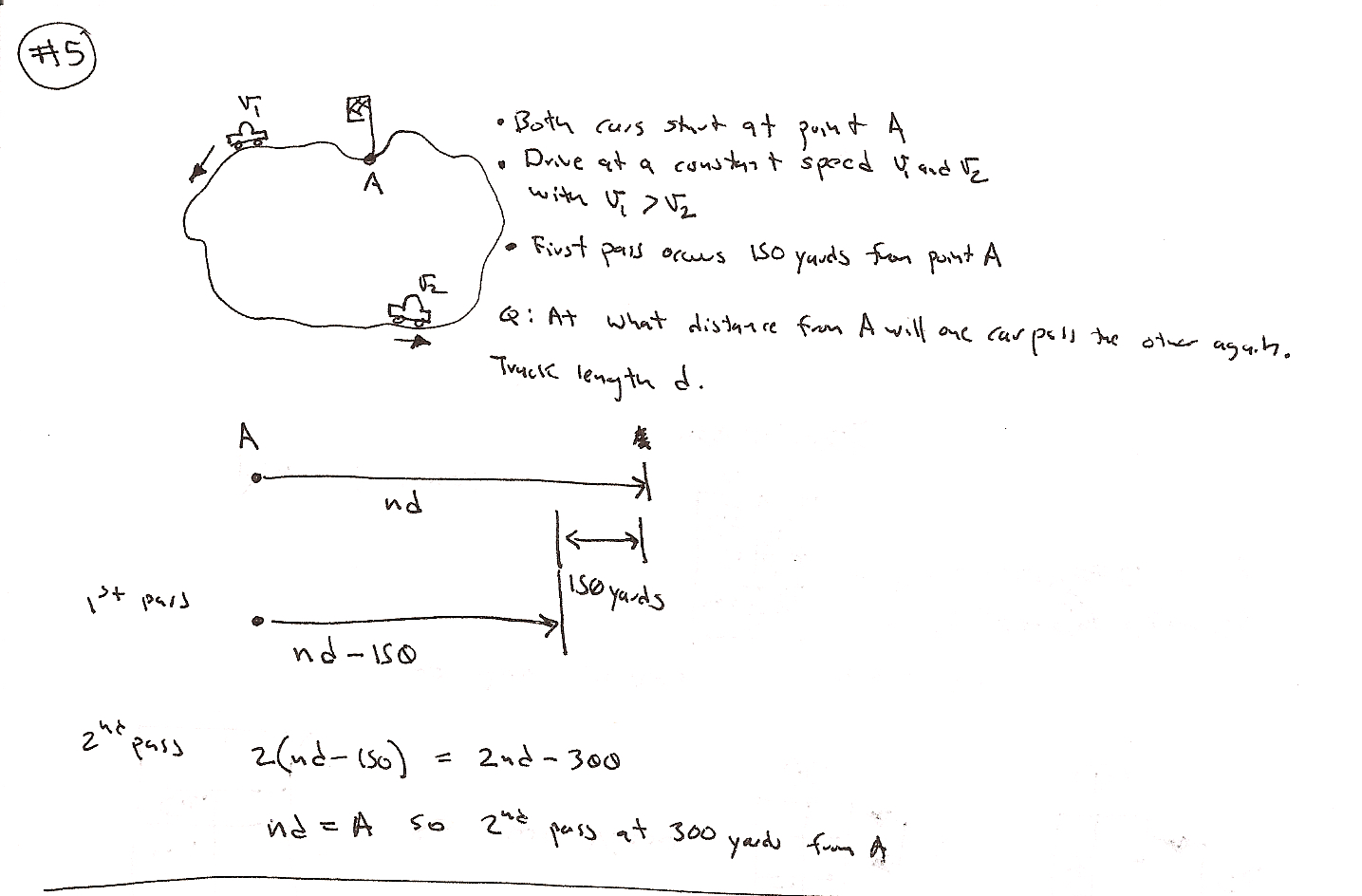
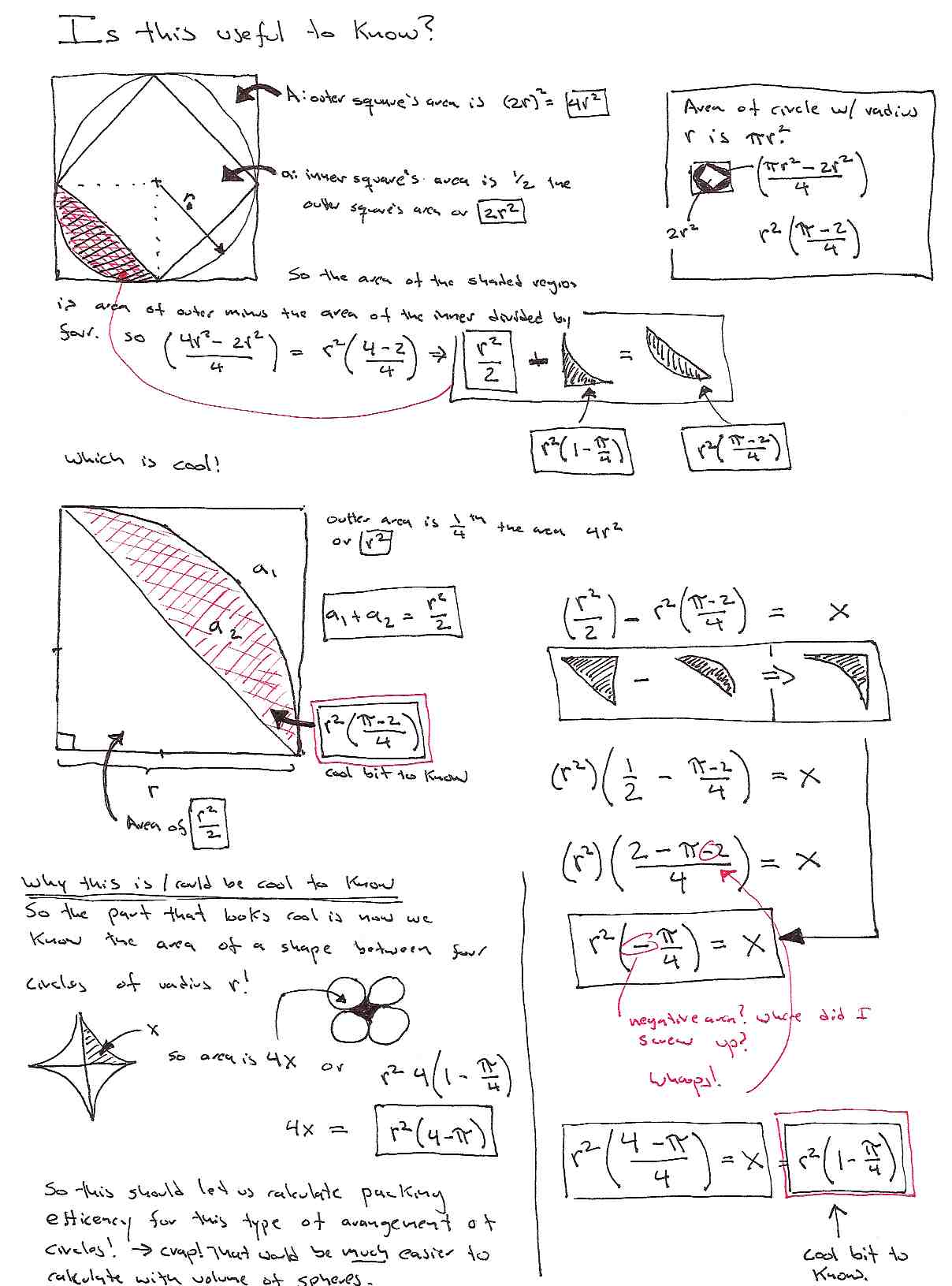
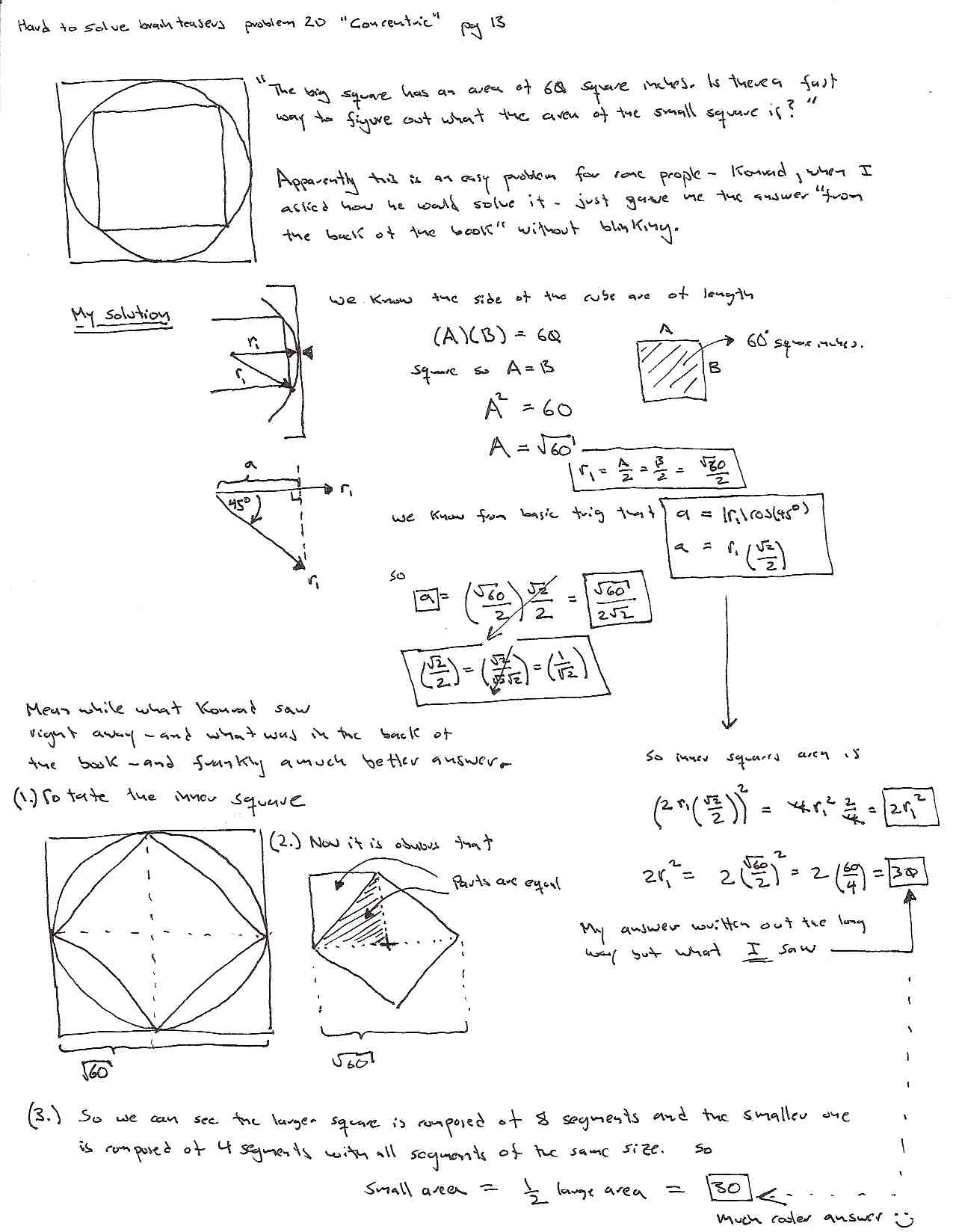
So after two years I finally tested for my green belt. It probably didn’t hurt that somehow Sensai’s polite suggestion of “You should be at the test this saturday” had apparently become “Be at the test this saturday – or else”. Ok. I added the “or else” part but I think it was fairly implicit from his tone and the look. So, yeah, I made sure I was at the test. Apparently Mr Moran was walking arround taking pictures, and posted them online. Nice of him – but it was weird – he must have been invisible for most of the test becuase I hardly noticed he was there at all. Then again – I guess that is a requirement for a good photographer.

So first, Mr Koons is officially the worst dance partner ever!

greenbelt_t4

On some of the throws he did work in a sweet joint lock on the elbow. I think it was an accident but I am going to certainly want to go back and look at that technique later when I have more control with my Karate.

So the danger of working out of your garage and interacting with people over the phone and the net? Well if you are not careful you can end up looking like me in these pictures. Grizzly Adams gone wrong.

: This picture made be immediatly go home and shave!

Oh, and the obligatory belt picture.

Uncategorized

“The tape roll”

Being a big fan of duct Jason has twelve brand new rolls out in the garage, but unfortunately none of them say how much tape is on a roll! To help Jason plan out a big duct tape project can you figure out how much tape is contained on each roll? You are able to measure that the tape is wrapped around a cardboard tube with an outer diameter of two inches, and that the tape wraps around the tube until it has an outer diameter of 3.5 inches. The tape measures out to be 0.01 inches thick. What length of tape is contained on each roll?

The wording needs a bit of work – specifically I want to add some reason why Jason wants to know how much tape is on each roll – but for now I am stumped. I originally wrote it with him wanting to make a suit out of duct tape for his high school reunion – but the absurdity eclipsed the problem. Eclipsing the problem is sort of an ongoing problem when I write this stuff up.

My main problem here, I think, is that it is a very simple problem if you have the tools to solve it – but I am not sure if it is too difficult if people have never worked with power series. I wrote up the solution as an introduction to them – and that is the goal of this problem: to get people thinking with power series.

As always my answer is on the book site I set up. The comments below are just for discussing the problem / people to post their answers.

Book Notes Lateral Thinking

An impossible game of catch?

Post author By Aaron
Post date February 22, 2010
4 Comments on An impossible game of catch?

Tristan and his friend Joe are playing a game of catch. They are fifty feet apart from each other and tossing the ball back and forth at approximately seventy-five feet per second. Two thirds of a second elapse between each of the throws of the ball and the corresponding catch. During that time the ball travels one hundred and sixty seven feet. How is this possible?

Ok, so my first attempt at a lateral thinking problem was a bit of a disaster. Konrad and Jason both were not happy with it and I am trying to figure out a way to re-work it so that the problem is not trying to figure out what the heck I am thinking!

Apparently since I want to publish I need to hold off on posting answers here for copy write reasons. So I will post the answers on a separate site and use comments here as a way to discuss the problems.

Book Notes

Book Notes: lateral thinking problem(s)

Post author By Aaron
Post date February 22, 2010
No Comments on Book Notes: lateral thinking problem(s)

So I hate “lateral thinking” problems. Seriously. They usually seem to be more of an exercise in thinking about how other people think – normally an interesting if not enjoyable topic – but somehow sucked dry of the positives of the experience. Never thought much about why I feel that way but I will certainly give it more thought now that I need to write some for my puzzle / math book.

So at some stage I need a tutorial on how to approach these sorts of problems algorithmically – to that end I wrote up this example.

A problem I found online for “lateral thinking” was stated as:

Problem: “How can you throw a ball such that it always comes back to you?”

I am paraphrasing the problem but this restatement has the critical property of the original – at least one answer that is obvious from reading it. Answer: “Throw the ball straight up!”.

These problems always have a basis set of assumptions. For example that the person is in a gravity field or on Earth, that that they can’t throw the ball at escape velocity. I broke down some examples below that have easy graphical representations of the problem. The graphics should help with the book and relaying understanding.

Book notes: examples on breaking down lateral thinking

Algrebra Programming

Correction – find missing / extra element in set of values 1..(N-1)

Post author By Aaron
Post date February 21, 2010
No Comments on Correction – find missing / extra element in set of values 1..(N-1)

So I already noted this correction in the previous post – but this is what they find a repeated / missing element in a collection of values from 1…N-1 should have looked like.

Correction - find a repeated / missing element in set of values 1..(N-1)

Just writing this problem down is making me realize how much I have forgotten. Time to crack open the books. I mean I even forgot my notation for mapping into a set with conditions!

Uncategorized

Sum of numbers from 1..N with one missing or one extra

Post author By Aaron
Post date February 21, 2010
No Comments on Sum of numbers from 1..N with one missing or one extra

[Update: This is why you dont write down things in the middle of the night… the sum I wrote up and *did not notice* is totally wrong. I also made an error on another problem I wrote down. Anyway, the error here is that the sum from 1 to N-1 does match with [((N-1)+1) + ((N-2)+2) + …] becomming N^2/2 not N/2. I just forgot to write down N^2, got distracted, then came back and finished it off that way. Crazy. Yet again I need to never do math after midnight. Anyway ignore what I wrote up below – essentially you have the same solution but the sum you compare with is N^2/2 for a list from 1…N-1 in value. Not going to delete the post as this makes a good example of a simple mistake that can even seem resonable if you dont doubble check your finial result! So might stick this in the book as an example of what NOT to do. ;-) ]

So when preparing for my Amazon interview I brushed back up on computer science as opposed to nocking the rust off my coding skills (read getting back to where I could code my way out of a paper bag). Anyway one of the things I ran across when prepping for the interview was a numeric sum problem. Basically you are given a list of numbers ranging in value from 1 to N, in unsorted order. One of the numbers is either missing or duplicated – write a number to find the function.

Sum of numbers from one to N with a missing or repeated value — ( Note: The above is totally wrong, and is an example of an error! See my update at the top of the post for the real answer!)

One solution is to sort the list and then search it for the missing / repeated value. Should be able to do this in O(nlogn) time. I need to check but I *think* a radix sort would work here for N time. A much better solution is to remember the series equivalent of 1…N. Then you can sum the numbers you were given, compare that number with the series equivalent, and just know the answer. Since it takes only one pass over the list it works in O(N) time too.

Algrebra Problems

Up and Down

This is another one from hard to solve brain teasers. It is just another algebra story problem that I have no idea why the included in the book. You just write down what they tell you as equations and end up with two linear equations with two unknowns – so it is fairly straightforward to solve . I do like the way they present the information here as it acts as a good example problem for introducing the idea of graphing or drawing a problem in order help set up equations to solve it.

It would still be a fairly simple problem to solve, but making the problem 3 equations in two unknowns, and using the extra information to nail one of several solutions might make it more fun. So one like this should go in the book.

Good example on graphical representations to solve a problem — Good example on graphically representing a story problem

Algrebra Problems

Irregular Circuit

So this was problem 5 from hard to solve brain teasers. I am working through the book and this problem is representative of about 60-70% of the problems which are just annoying. This would not be a hard problem in a 6th or 7th grade algebra course. I am fairly sure the book is targeted at adults – so are these problems hard because you are supposed to not remember junior high? Ugh.

The problem:

“Two cars start from point A at the same time and drive around a circuit more than one mile in length. While they are driving laps around the circuit, each car must maintain a steady speed. SInce one car is faster than the other, one car will pass the other at certain points. The first pass occurs 150 yards from point A.

At what distance from A will one car pass the other again?”

The thing I don’t like about this problem is it really is just a story problem where you just get the answer reading it. How? Because the problem lacks enough information to have any other way to set it up. You either get that starting at 0 and ending at A away from 0 means the second pass will be 2A away from the origin as long as the track is longer than 4A in length.

This could be turned into an interesting problem if the speed around the track was not constant in such a way that for the Nth lap A would be in the lead, for the Mth B would be in the lead. Then knowing who wins the race would require knowing the track length. If that was not given but was instead easily calculable the way to solve the problem would not jump out so much. I will have to try and write up a version like that for the book.

Update: Interesting – the problem directly before this one in the book is the same problem class I was proposing to modify this too. I wonder if the author was thinking that when clustering these problems of if that was just on my mind since I just solved that problem two hours ago or so. Huh.

Geometry

Is this useful to know?

So after that last problem I got to thinking that the area between a circle and its bounding or contained square would be potentially useful to know. Really. It just seemed cool. Only problem is that every use for it I could think of I could think of other ways to get there. Grrrr. Is this really cool – or is it the mathematical equivalent of carrying around a small dog in a shoulder bag?

Geometry Logic Problems

Mathematicians suck!

Finally I have some time to work through daily problems again. Worked this one last week and forgot to write it up.

When I saw this problem I just saw the trigonometry solution and it blinded me to the symmetry. I guess math is good at showing how what we already know can blind us to the better paths.

So why do mathematicians suck? Well that seemed politer for Konrad than saying he sucks – I worked on this problem for a while and just did not see it. He saw the answer before I was finished describing the problem. So I guess I am the one who sucks, – apologies to mathematicians everywhere.

Area of a square - inside a circle - inside a square