 .
.
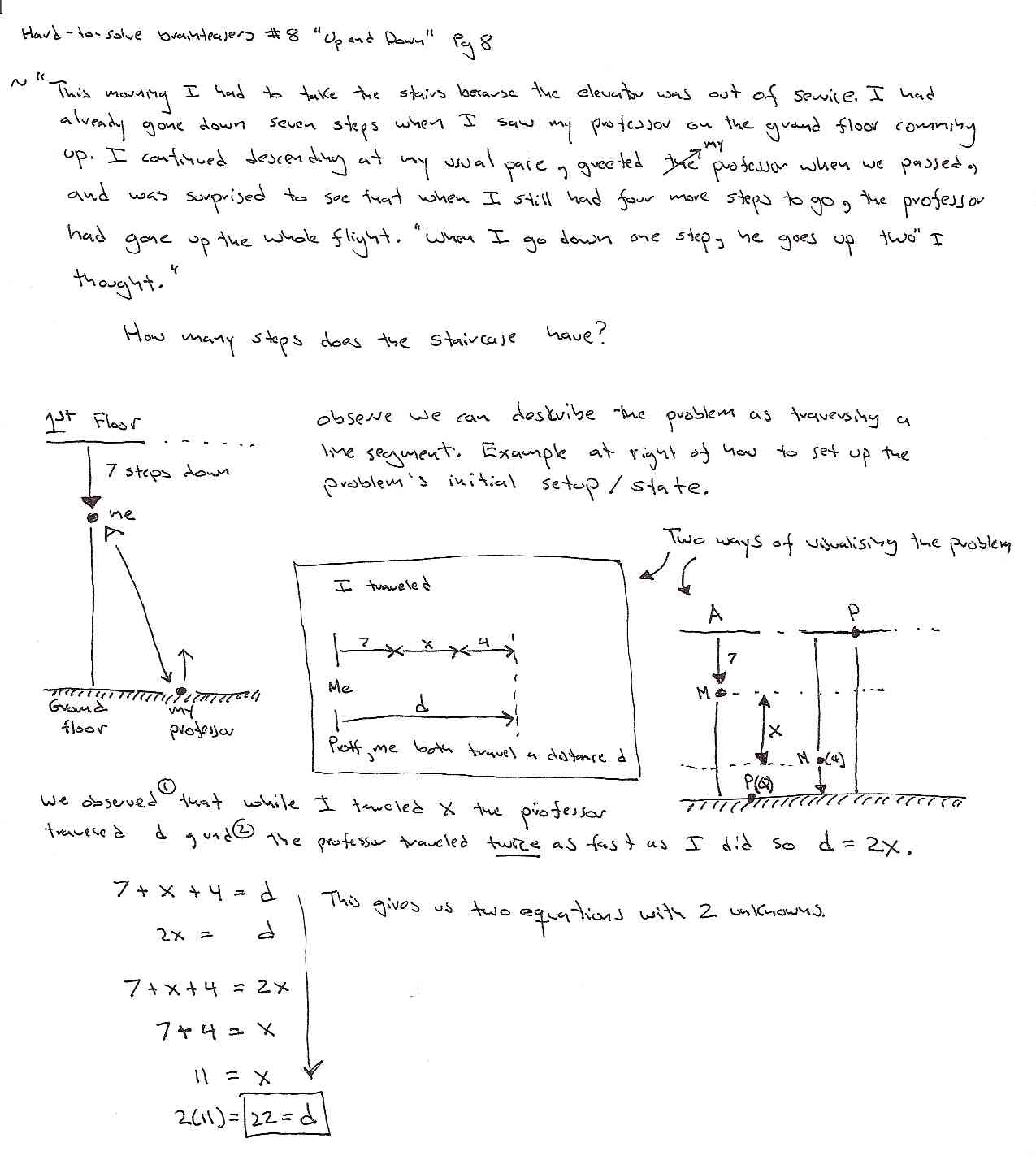
So this is just an algebra story problem. We know that the staircase has the seven steps the person had already walked down when he saw his professor, some number of steps that are unknown we label as x, and four steps that were remaining when the professor had traveled the staircase. So we know that the staircase has 7 + x + 4 stairs.
We also know that both the professor and the student travel the
same number of steps we can label as a distance d, and that the
professor travels the steps twice as fast as the student. So
this gives us two equations with two unknowns:
EQ1: 7+x+4 = d
EQ2: 2x = d
So solving 7+x+4 = 2x gives a value of 11 for x, and because of equation D we know the staircase has 22 steps. We check out answer by plugging into EQ1 we see 22-7-4 = 11, so the student walks 11 steps for the professors 22.