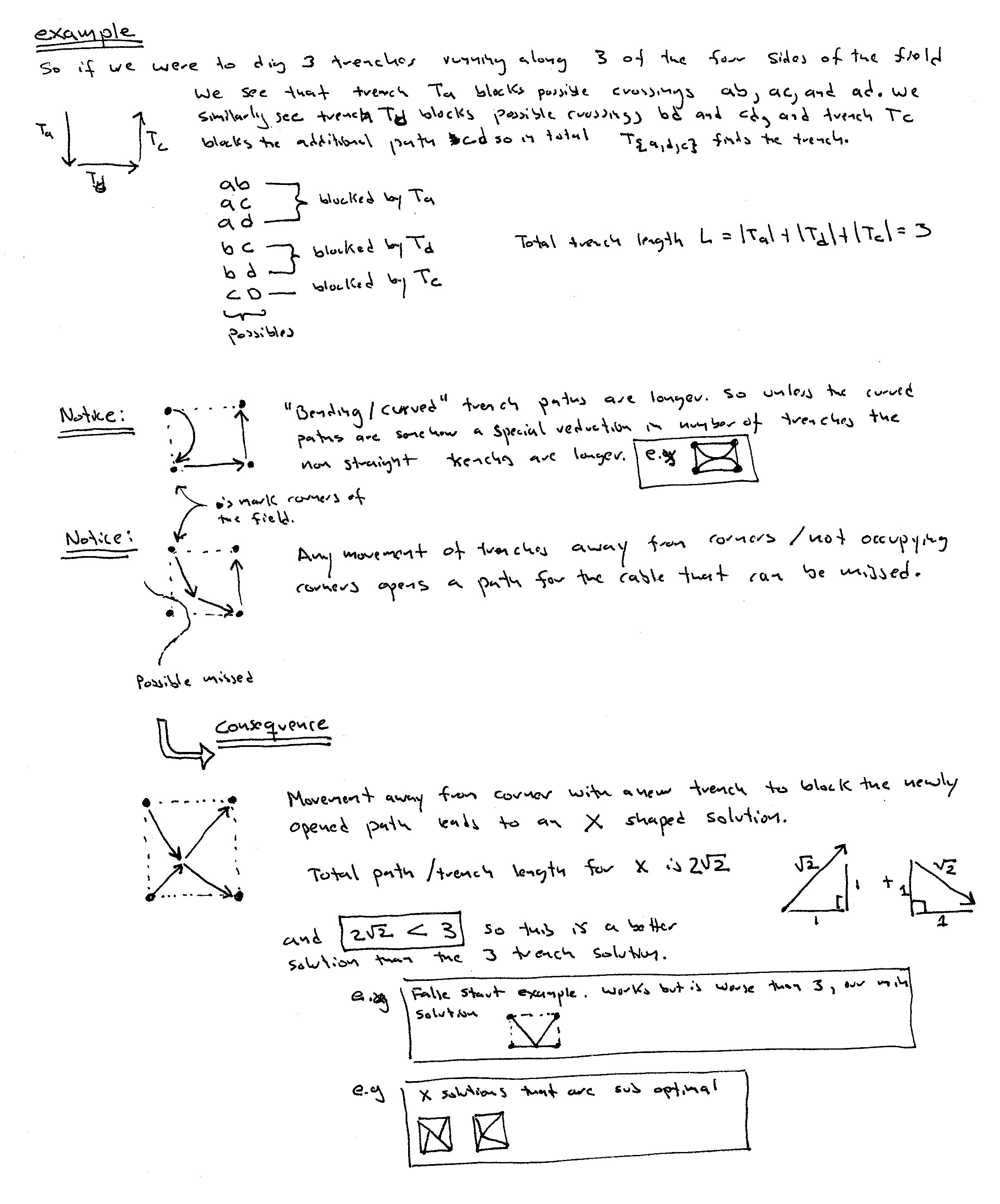
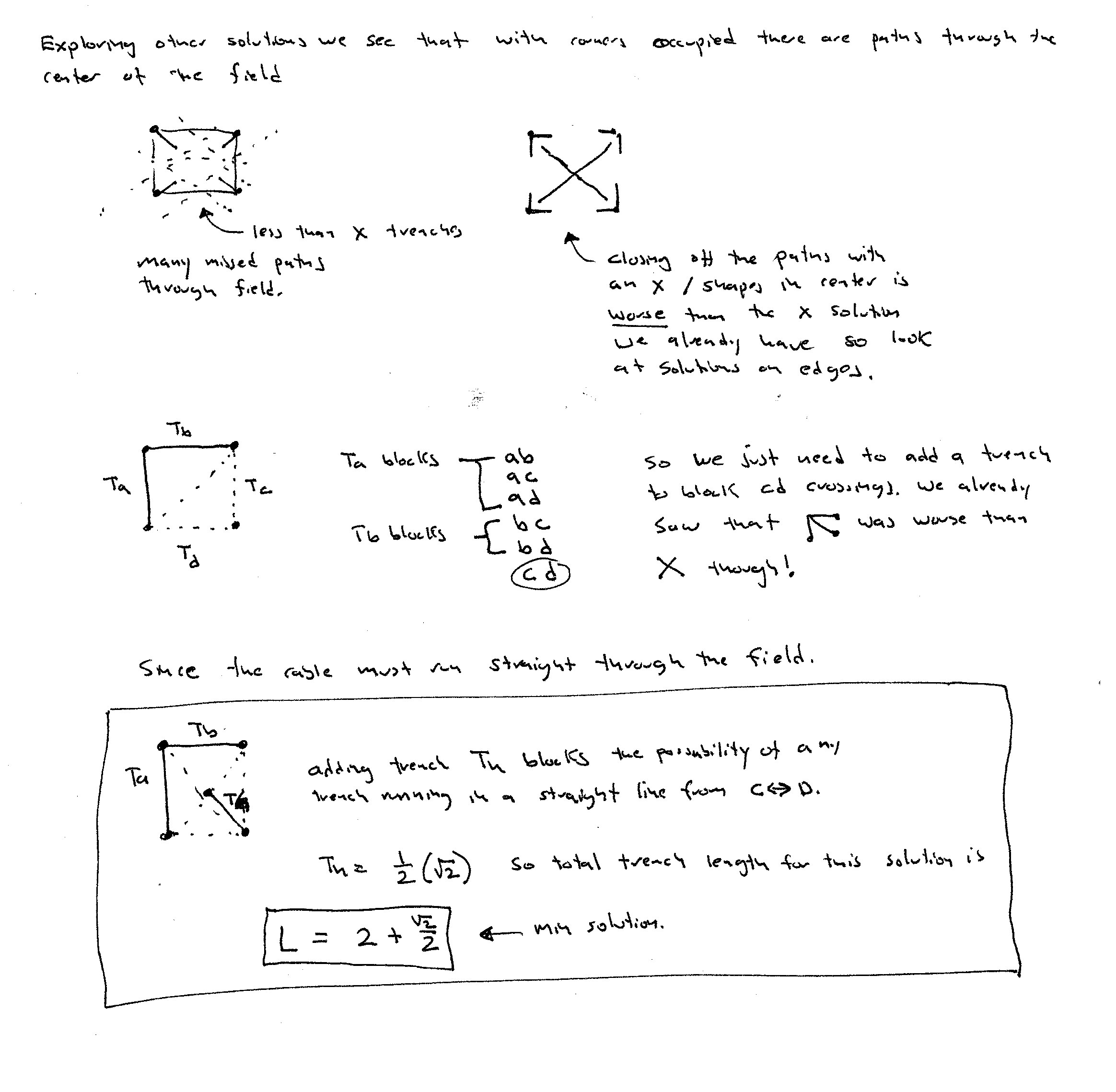
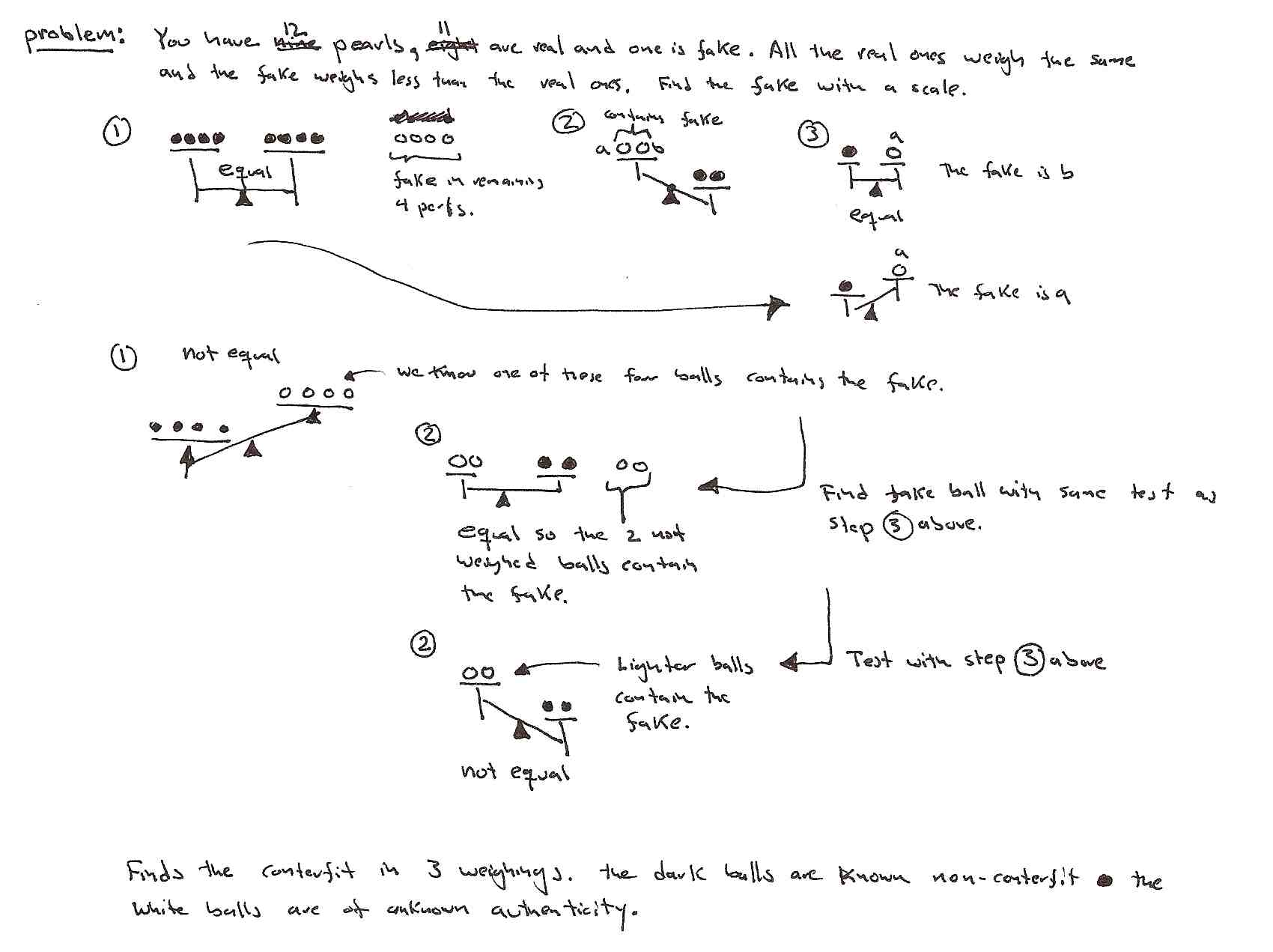
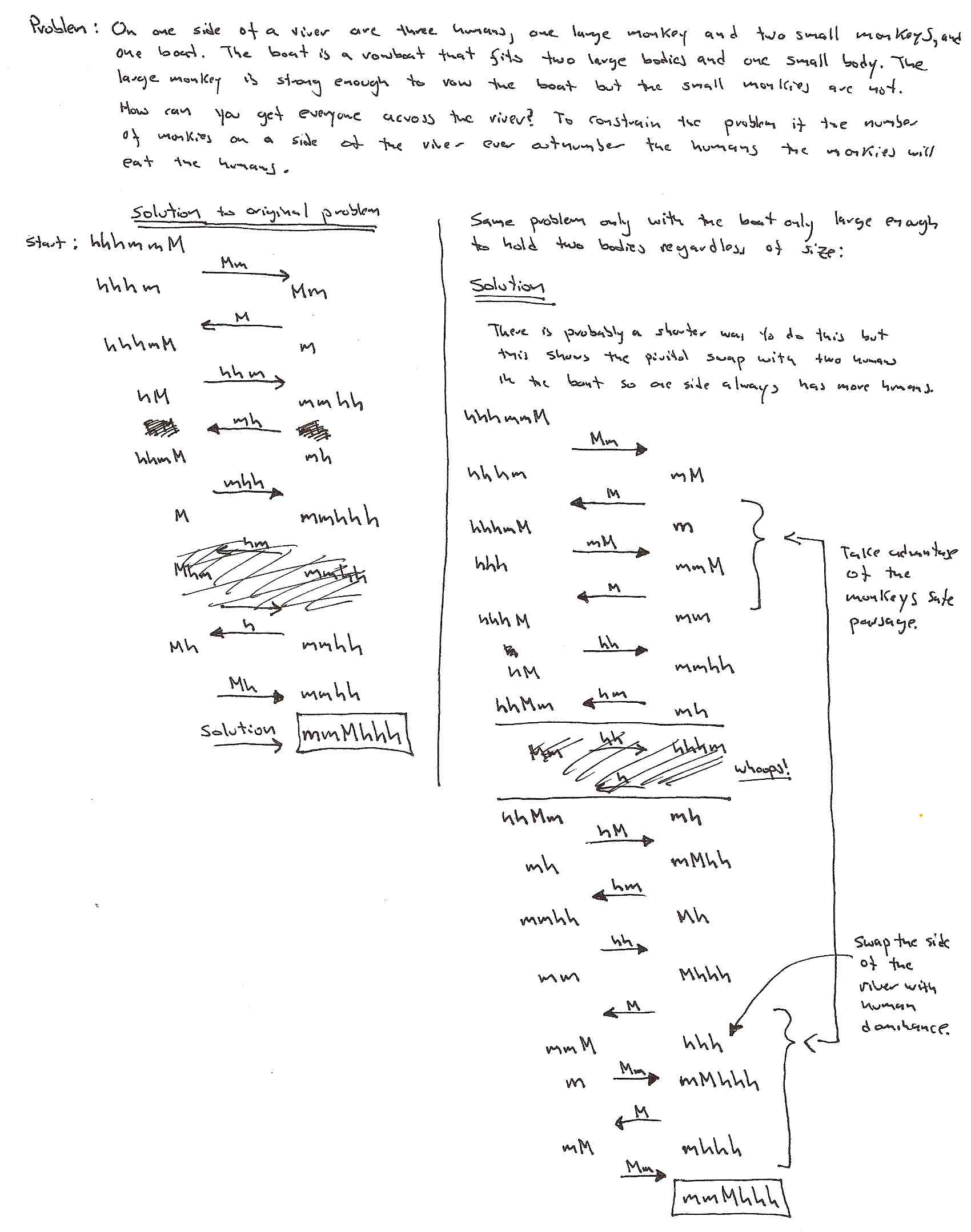
Problem 179 from http://mathproblems.info/group9.html
A drag racer accelerates at a uniform rate from its starting point. It travels the last one fourth of the distance from the starting point to the finish line in 3 seconds. How long did it take to travel the entire distance from starting point to finish line?
Problem nummber 110 from http://mathproblems.info/group6.html
There is a straight cable buried under a unit square field. You must dig one or more ditches to locate the buried cable. Where should you dig to guarantee finding the cable and to minimize digging? For example you could dig an X shape for total ditch length of 2*sqr(2) but there is a better answer.
Solution….
continuing…
continuing…
Problem 85 from http://mathproblems.info/group5.html
In front of you are 12 pearls, 11 being real and one fake. The real ones all weigh the same and the fake one differs in weight from the real ones (may weigh more or less). With a balance scale and three weighings how can you weed out the fake one and determine whether it is too heavy or too light?
Problem 79 from http://mathproblems.info/group4.html
One one side of a river are three humans, one big monkey, two small monkeys, and one boat. Each of the humans and the big monkey are strong enough to row the boat. The boat can fit one or two bodies (regardless of size). If at any time at either side of the river the monkeys outnumber the humans the monkeys will eat the humans. How do you get everyone on the other side of the river alive?
Saw this problem at http://gurmeetsingh.wordpress.com/puzzles/
A man is trapped atop a building 200m high. He has with him a rope 150m long. There is a hook at the top where he stands. Looking down, he notices that midway between him and the ground, at a height of 100m, there is a ledge with another hook. In his pocket lies a Swiss knife. Hmm… how might he be able to come down using the rope, the two hooks and the Swiss knife
I found PDF file talking about MERSA in wrestling / contact sports.
Implement insert for a binary tree
Implement an algorithm to insert in a sorted list.
Delete an element from a doubly linked list.
Devise an algorithm for detecting when a string is a palindrome. Ex: A man, a plan, a canal, Panama”.
(Another from: http://www1.cs.columbia.edu/~kns10/interview/)
Example palindromes I got from a quick web search.