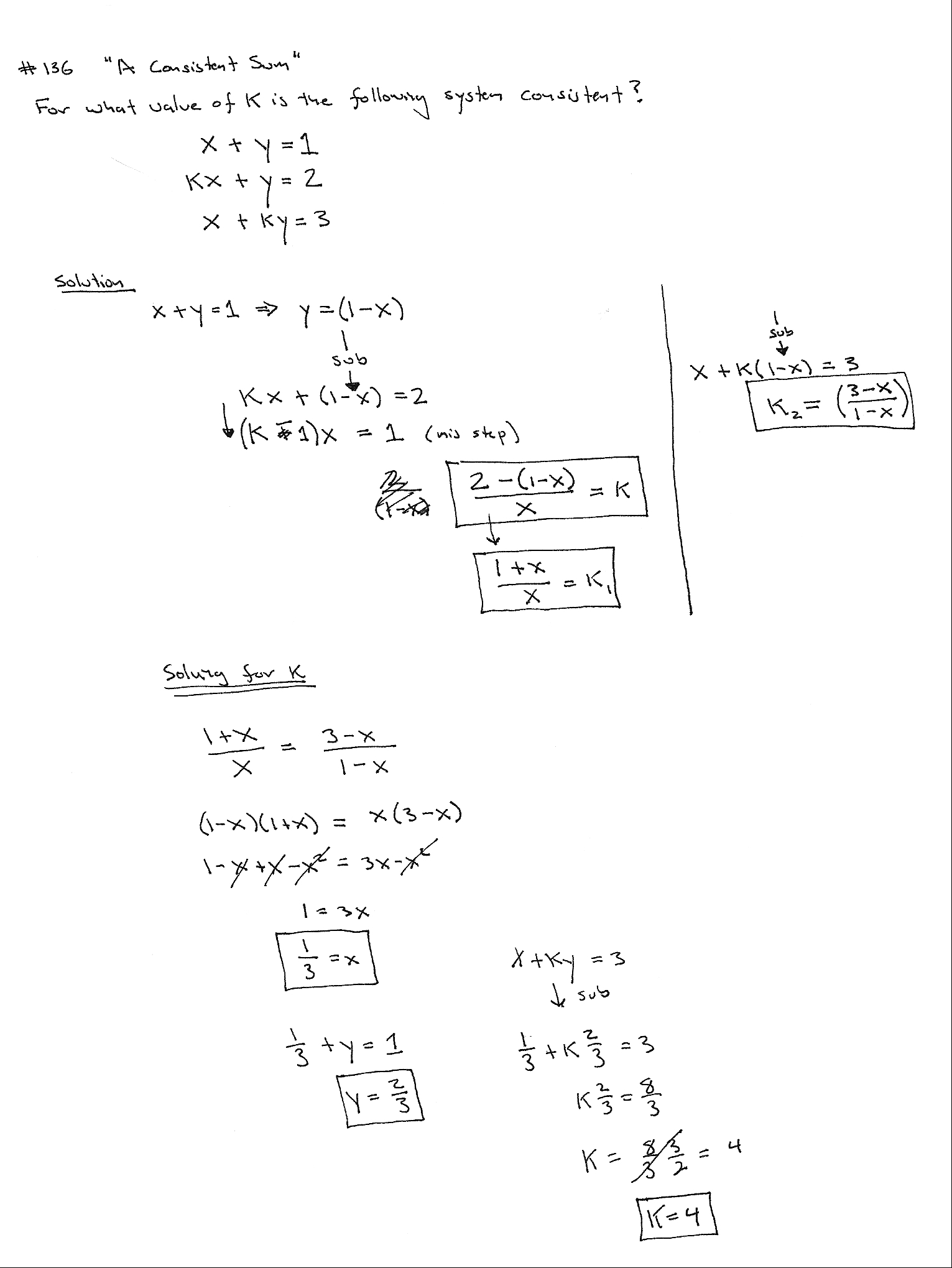
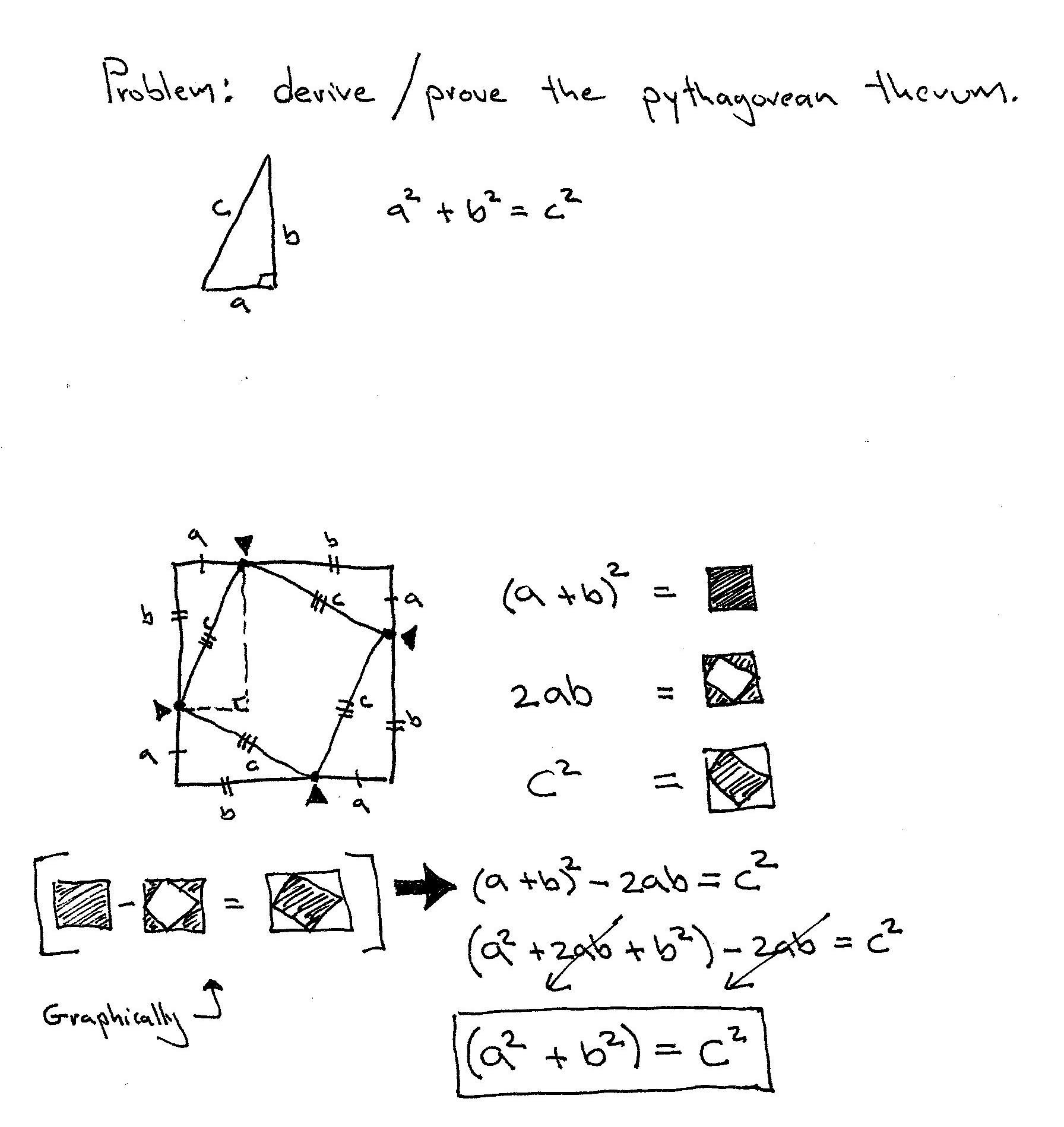
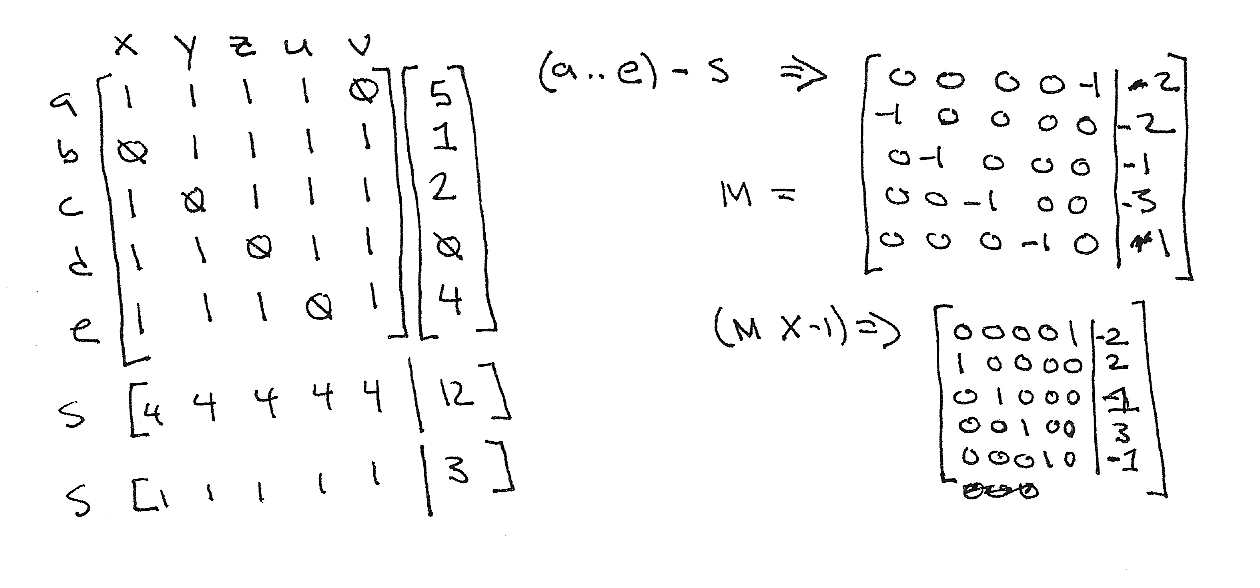Sensai taught this technique last thursday (May 28th) – unfortunately I did not write it down right away and now that I sat down to capture it the details are fuzzy. The technique is a reversal, starting from a bottom position nage escapes the mount and puts uke in an arm-bar. The figure shows Nage putting an arm bar on Uke’s right hand
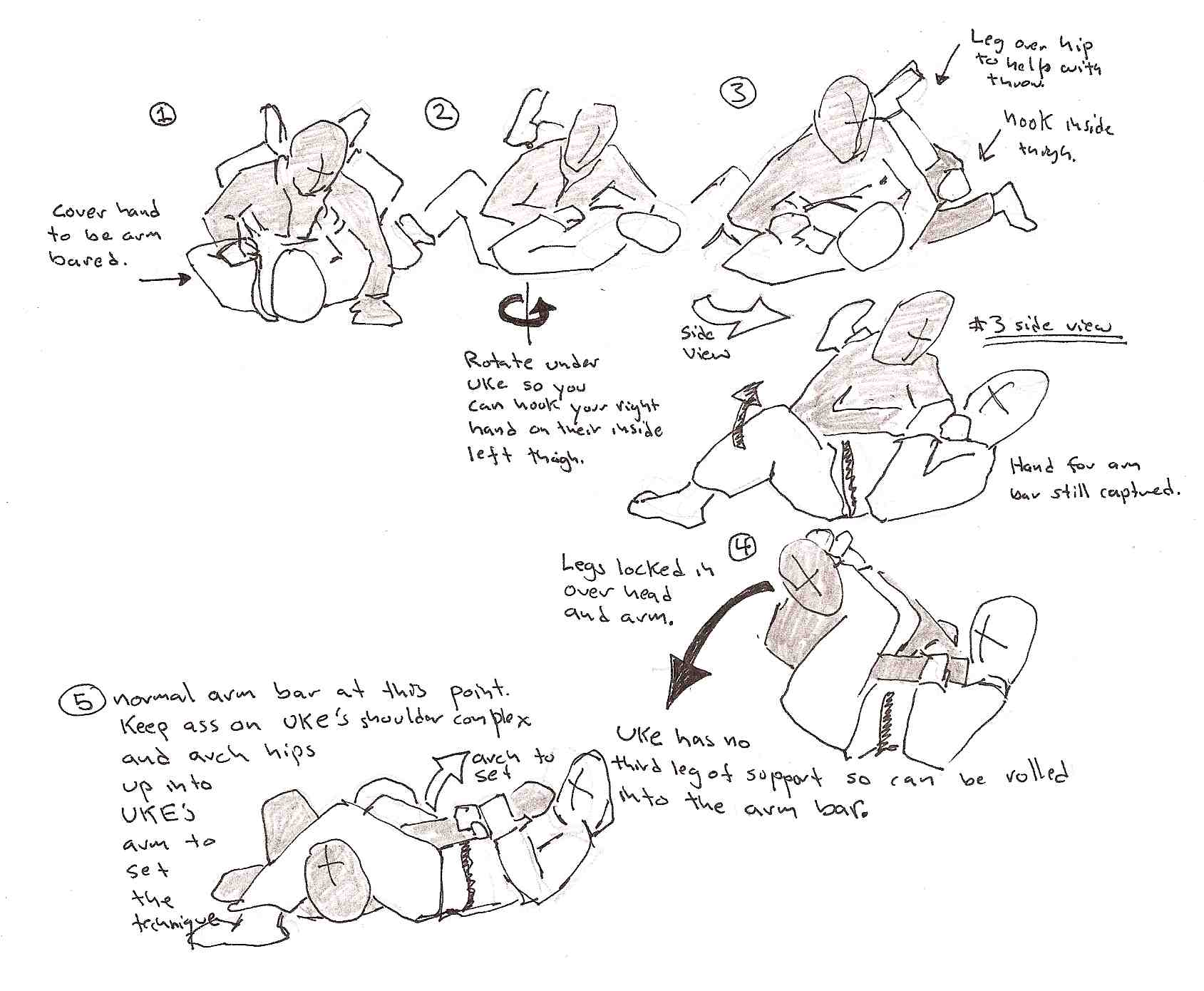
Step one
To start the technique Nage captures Uke’s right hand – immobilizing it on his chest with his left hand. If Uke is setting up Nage for a technique that starts with a lapel grab – like a deep collar choke – that lapel grab sets up Uke for the technique. So this technique should make for a counter.
As part of setting the escape up Nage makes sure the leg on the side he is arm baring is on Uke’s hip or higher. So if Nage is arm-barring Uke’s right arm then Nage’s right leg is on Uke’s left hip as shown in the figure.
Step two and three
Nage wants to rotate under Uke. Nage does a hip out under Uke. At the same time Nage hooks Uke’s inner thigh with his right hand. This hook lets Nage spin under Uke as opposed to the escaping movement a normal hip out would cause.
Step four
Nage raises his outer leg and hooks it over Uke’s neck. Since Nage still has Uke’s arm immobilized Uke is basically a tripod and unstable. So with Uke’s head hooked Nage can flip Uke over onto his back with just the leg hook.
Step five
Uke’s shoulder and torso should be touching Nage’s rear, if it is not Nage may have to slide his body forward. Uke’s arm runs through Nage’s groin with Uke’s upper arm resting on Nage’s pelvic bone. Nage’s hip forms the base of a fulcrum formed by Uke’s arm so it is important that the arm is resting on the hip bone and prevented from moving side to side by being sandwiched between Nage’s Legs. Nage sets the technique by arching his hips into the technique – this applies force on the joints using Uke’s arm as a leaver.
The seated arm bar is a joint technique executed on both the shoulder complex and elbow. So the arm needs to be straight so the technique locks out both the elbow joint as well as the shoulder.