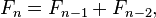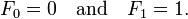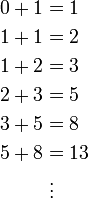This blog post was awesome. I am working through a lot of TensorFlow material lately and it was refreshing and atypical to find someone telling you what not to do.
I am capturing it here so I can find it again in the future. If you are interested in TensorFlow, or technical writing, this is worth a read: How Not To Program the TensorFlow Graph
Danijar Hafner has an excellent tutorial on Structuring Your TensorFlow Models. I really liked it so I am posting it here so its always easy to find. He is using Python’s decorators to provide a lazy initialization for the graph components. Its a neat trick. Totally separate from TensorFlow, I am actively working on improving my Python programming and will definitely be using this approach in the future.
I’ll admit – I still try and write Python like it was C or C++. To fix that for a while I am going to switch to writing things in Python for a while, while working on actually writing good Python.
Graph algorithms are the kidneys of computer science – there in the background filtering out all the bad things for us. In my switch over to writing in Python I needed to find a solid python graph library, and decided to try NetworkX. Here is a simple example program using it. These are mostly just notes for myself – but I am posting it here in case it is useful to anyone else.
This code is basically the NetworkX weighted graph example, with some annotations. Here is some code to create and plot a weighted graph.
import matplotlib.pyplot as plt
import networkx as nx
# Populate the graph...
map_graph = nx.Graph()
map_graph.add_edge('Issaquah','Bellevue', weight=0.11 )
map_graph.add_edge('Bellevue','Kirkland', weight=0.05 )
map_graph.add_edge('Bellevue','Redmond', weight=0.06 )
map_graph.add_edge('Kirkland','Redmond', weight=0.24 )
map_graph.add_edge('Bellevue','Seattle', weight=0.01 )
map_graph.add_edge('Renton','Seattle', weight=0.03 )
map_graph.add_edge('Renton','Bellevue', weight=0.48 )
# Determine the layout of points in the graph. Some other layouts that
# would work here are spring_layout, shell_layout, and random_layout
pos = nx.circular_layout( map_graph ) # Sets positions for nodes
# Put "dots" down for each node
nx.draw_networkx_nodes( map_graph, pos, node_size=700)
# Attaches Labesl to each node
nx.draw_networkx_labels( map_graph, pos, font_size=14, font_family='sans-serif')
map_edges = [(u,v) for (u, v, d) in map_graph.edges(data=True) ]
nx.draw_networkx_edges( map_graph,
pos, # Spring
map_edges, # List of edges
width=5, alpha=0.5, edge_color='b', style='dashed' )
plt.axis('off')
plt.show()
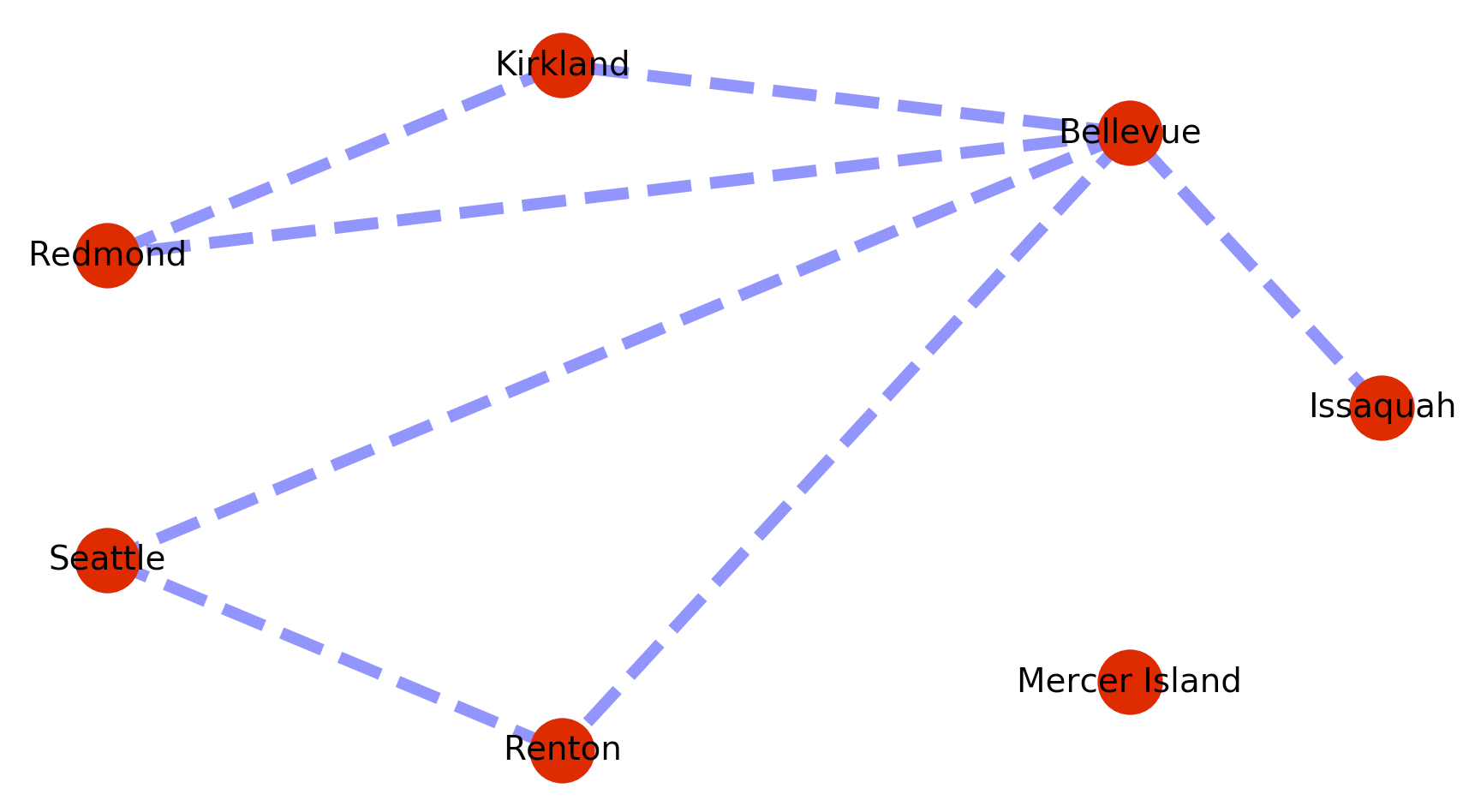
The plotted graph looks something like this.
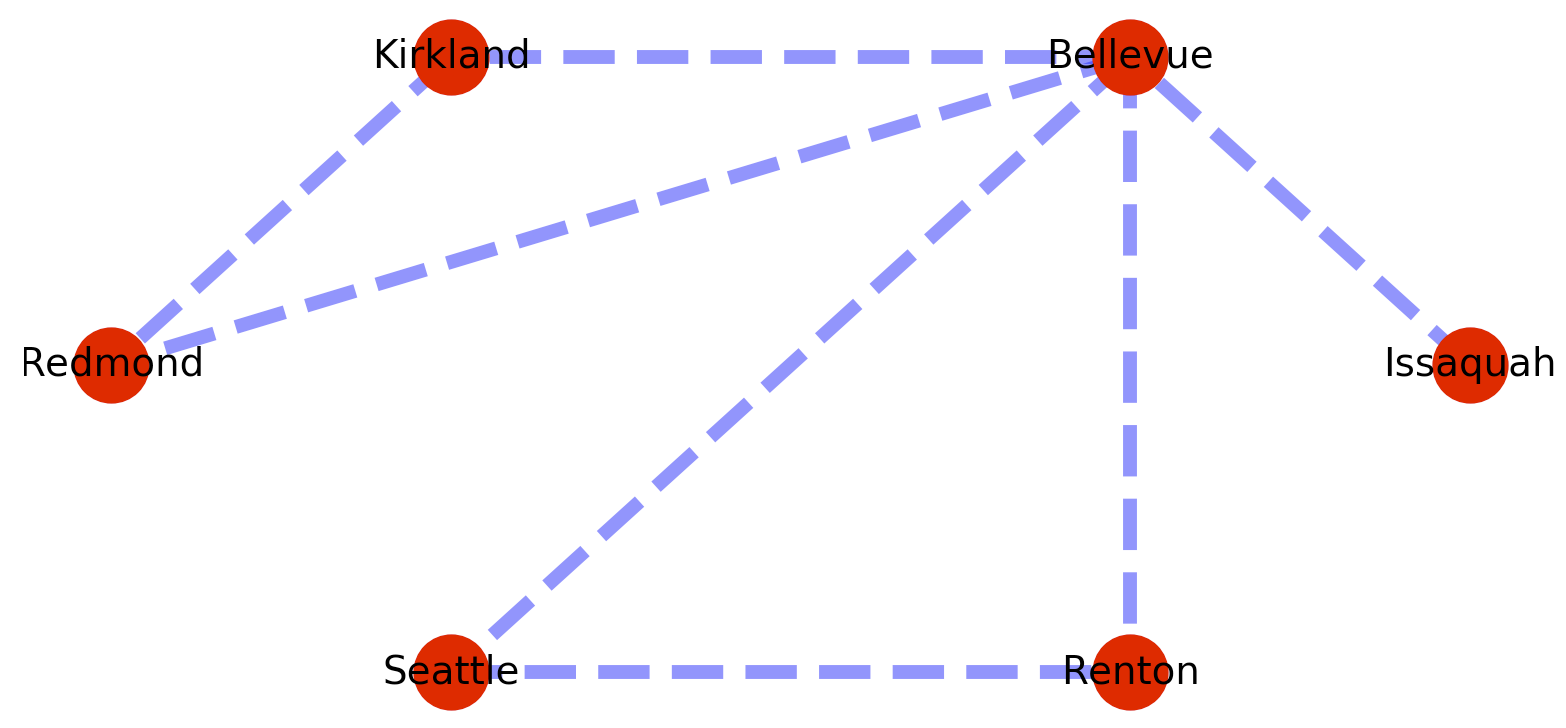
One of the things I want from a graph library is the standard graph algorithms – like finding me the shortest path between nodes, or testing for the presence of a path at all. So for example to find the shortest path from Issaquah to Renton we could add the following code to the example above?:
# Generates the shortest path - but since there could be more than
# one of them what you get back is a "generator" from which you
# need to pluck the shortest path.
a_shortest_path = nx.all_shortest_paths(map_graph, source='Issaquah', target='Renton')
print( [p for p in a_shortest_path] )
The added code will give the path [[‘Issaquah’, ‘Bellevue’, ‘Renton’]], which is the shortest path by number of edges traversed. To obtain the shortest path by edge weight we can use dijkstras like so:
a_shortest_path = nx.dijkstra_path(map_graph, ‘Issaquah’, ‘Renton’)
print( a_shortest_path )
Which gives the path: [‘Issaquah’, ‘Bellevue’, ‘Seattle’, ‘Renton’]
The problem is that this implementation of dijkstra’s fails when a path is not present between the origin and destination nodes. So for example if we add a disconnected vertex with no edges like below, searches on a path to that vertex will cause the call to fail.
map_graph.add_node(‘Mercer Island’)
I think you need to use the has_path method to test for the existence of any path first, then if there is a path use dijkstras to find the minimum cost path. Something like this:
# Create a helper function for testing for a path
def shortest_weighted(from_node, to_node):
if nx.has_path( map_graph, from_node, to_node ) == True :
a_shortest_path = nx.dijkstra_path(map_graph, from_node, to_node)
return( a_shortest_path )
else:
print("No path from",from_node,"to", to_node, "\r\n")
return( False )
Then checking for the minimum path can look something like this:
# Test where path does not exist
shortest_weighted_path = shortest_weighted( 'Issaquah', 'Mercer Island' )
if shortest_weighted_path != False:
print( shortest_weighted_path )
# Test where path does exist
shortest_weighted_path = shortest_weighted( 'Issaquah', 'Renton' )
if shortest_weighted_path != False:
print( shortest_weighted_path )
Neither call will fail and checking for the existing path from Issaquah to Renton will return: [‘Issaquah’, ‘Bellevue’, ‘Seattle’, ‘Renton’]
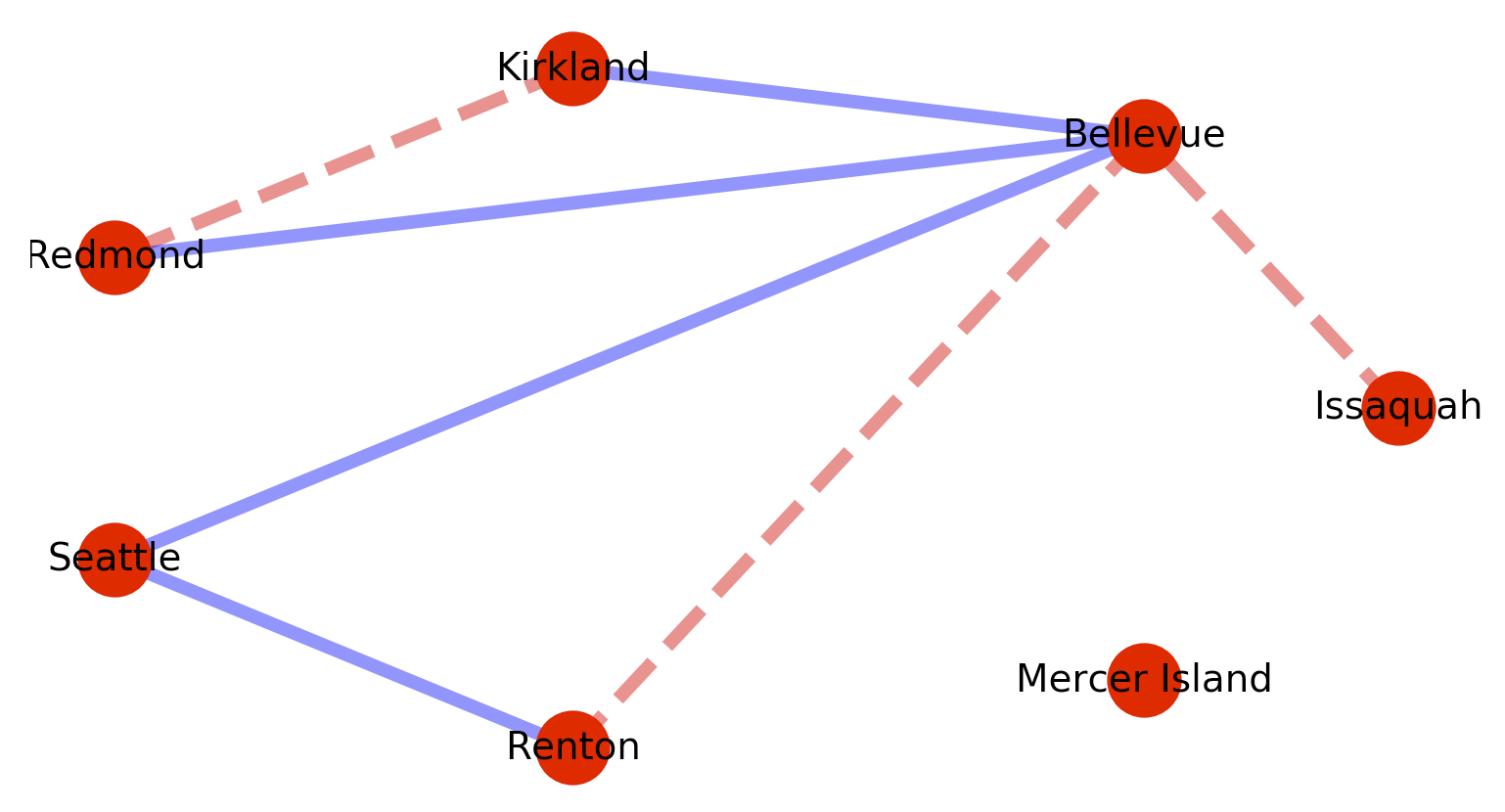
Since the graphs are weighted – list comprehensions can be used to conditionally act based on edge weights. For example:
# Segment the nodes by weight
map_red_edges = [(u,v) for (u, v, d) in map_graph.edges(data=True) if d['weight'] > 0.1 ]
map_blue_edges = [(u,v) for (u, v, d) in map_graph.edges(data=True) if d['weight'] <= 0.1 ]
Then use the segmentation to perform multiple colorings.
nx.draw_networkx_edges( map_graph,
pos, # Spring
map_red_edges, # List of edges
width=5,
alpha=0.5,
edge_color='r',
style='dashed' )
nx.draw_networkx_edges( map_graph,
pos, # Spring
map_blue_edges, # List of edges
width=5,
alpha=0.5,
edge_color='b',
style='solid' )
Which will produce the following graph:
Also useful is shortest_path, which returns all the paths between all nodes, but sorted by vertex traversal path length. So the following code:
paths = nx.shortest_path(map_graph)
print( paths )
Generates the following paths.
{'Issaquah': {'Issaquah': ['Issaquah'], 'Bellevue': ['Issaquah', 'Bellevue'], 'Kirkland': ['Issaquah', 'Bellevue', 'Kirkland'], 'Redmond': ['Issaquah', 'Bellevue', 'Redmond'], 'Seattle': ['Issaquah', 'Bellevue', 'Seattle'], 'Renton': ['Issaquah', 'Bellevue', 'Renton']}, 'Bellevue': {'Bellevue': ['Bellevue'], 'Issaquah': ['Bellevue', 'Issaquah'], 'Kirkland': ['Bellevue', 'Kirkland'], 'Redmond': ['Bellevue', 'Redmond'], 'Seattle': ['Bellevue', 'Seattle'], 'Renton': ['Bellevue', 'Renton']}, 'Kirkland': {'Kirkland': ['Kirkland'], 'Bellevue': ['Kirkland', 'Bellevue'], 'Redmond': ['Kirkland', 'Redmond'], 'Issaquah': ['Kirkland', 'Bellevue', 'Issaquah'], 'Seattle': ['Kirkland', 'Bellevue', 'Seattle'], 'Renton': ['Kirkland', 'Bellevue', 'Renton']}, 'Redmond': {'Redmond': ['Redmond'], 'Bellevue': ['Redmond', 'Bellevue'], 'Kirkland': ['Redmond', 'Kirkland'], 'Issaquah': ['Redmond', 'Bellevue', 'Issaquah'], 'Seattle': ['Redmond', 'Bellevue', 'Seattle'], 'Renton': ['Redmond', 'Bellevue', 'Renton']}, 'Seattle': {'Seattle': ['Seattle'], 'Bellevue': ['Seattle', 'Bellevue'], 'Renton': ['Seattle', 'Renton'], 'Issaquah': ['Seattle', 'Bellevue', 'Issaquah'], 'Kirkland': ['Seattle', 'Bellevue', 'Kirkland'], 'Redmond': ['Seattle', 'Bellevue', 'Redmond']}, 'Renton': {'Renton': ['Renton'], 'Seattle': ['Renton', 'Seattle'], 'Bellevue': ['Renton', 'Bellevue'], 'Issaquah': ['Renton', 'Bellevue', 'Issaquah'], 'Kirkland': ['Renton', 'Bellevue', 'Kirkland'], 'Redmond': ['Renton', 'Bellevue', 'Redmond']}, 'Mercer Island': {'Mercer Island': ['Mercer Island']}}
As part of the latest skills review – I am going back over my coding and trying to get better. Being honest I have been pleasantly surprised, but embarrassed, by some of the places I have found I have room for improvement. It is worth it though – cause sometimes you catch gems like this.
When traversing trees, I tend to traverse them like they were graphs, and using queues. So for the problem of traverse a binary tree (not a BST), and return the largest value in each row I wrote the following code:
vector largestValues(TreeNode* root) {
vector maxrowval;
if( root == NULL )
return(maxrowval);
queue > treesearch;
treesearch.push(make_pair(root,0));
while( !treesearch.empty()){
TreeNode* curNode = treesearch.front().first;
int curDepth = treesearch.front().second;
treesearch.pop();
if( maxrowval.size() <= curDepth ){
maxrowval.push_back(curNode->val);
}
if( maxrowval[curDepth] < curNode->val ){
maxrowval[curDepth] = curNode->val;
}
if( curNode->left != NULL ){
treesearch.push(make_pair(curNode->left, curDepth+1));
}
if( curNode->right != NULL ){
treesearch.push(make_pair(curNode->right, curDepth+1));
}
}
return( maxrowval );
}
What I just ran across was someone who wrote the following code for the same problem. He is using a list as opposed to a queue – but the logic of what we are doing is about the same. Only his double nested loop traversal of the list should be much faster. It avoids a lot of pushing and popping operations, and leaves the constructed search list intact. I am posting this here so I can come back and look at this later. This is the kind of thing I am going to want to stew on and see where else it might be a useful thing to have in the toolbox.
vector largestValues(TreeNode* root) {
vector result;
list current;
if (root != nullptr) {
current.push_back(root);
}
while (current.size()) {
int max_value = INT_MIN;
int size = current.size();
while (size) {
TreeNode* node = current.front();
max_value = max(max_value, node->val);
current.pop_front();
if (node->left != nullptr) {
current.push_back(node->left);
}
if (node->right != nullptr) {
current.push_back(node->right);
}
size--;
}
result.push_back(max_value);
}
return result;
}
So I already noted this correction in the previous post – but this is what they find a repeated / missing element in a collection of values from 1…N-1 should have looked like.
Just writing this problem down is making me realize how much I have forgotten. Time to crack open the books. I mean I even forgot my notation for mapping into a set with conditions!
Same technique can be used to find loops in a liked list. If you advance through the list one pointer at rate X, and another pointer through the list at rate (1/2)X then when the faster pointer is at the end of the list the slower pointer will be pointing to the center element of the list.
<pre class=code>
// findCenterElement – finds the element at the center of the list
node *findCenter(node *curList){
node *centerNode = curList;
node *curNode = curList;
if(curList == (node *)NULL)
return((node *)NULL);
if(curNode->next != (node *)NULL){
while(((curNode->next)->next) != (node *)NULL)
{
curNode = (curNode->next)->next;
centerNode = (centerNode->next);
}
}else{
return(curNode);
}
return(centerNode);
}
</pre>
The way I found the problem on the web:
Give me an algorithm to shuffle a deck of cards, given that the cards are stored in an array of ints.
Write a function to print the Fibonacci numbers.
The fibonacci sequence is a set of numbers formed by
with seed values
This generates the numbers using the following set of rules….
So the fibonacci sequence is 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…