Category: Puzzles

Problem nummber 110 from http://mathproblems.info/group6.html

There is a straight cable buried under a unit square field. You must dig one or more ditches to locate the buried cable. Where should you dig to guarantee finding the cable and to minimize digging? For example you could dig an X shape for total ditch length of 2*sqr(2) but there is a better answer.

Solution….

continuing…

continuing…

Saw this problem at http://gurmeetsingh.wordpress.com/puzzles/

A man is trapped atop a building 200m high. He has with him a rope 150m long. There is a hook at the top where he stands. Looking down, he notices that midway between him and the ground, at a height of 100m, there is a ledge with another hook. In his pocket lies a Swiss knife. Hmm… how might he be able to come down using the rope, the two hooks and the Swiss knife

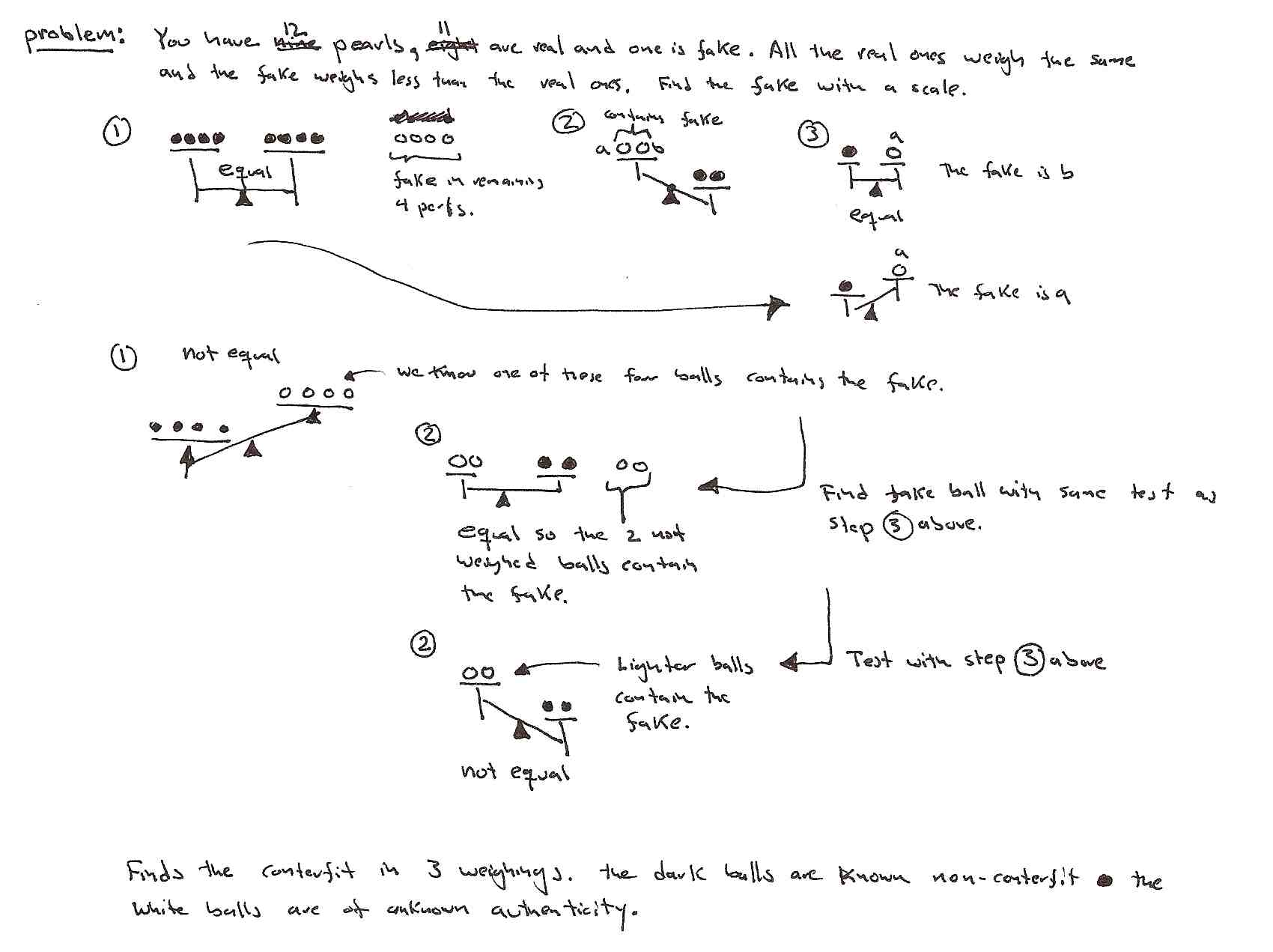
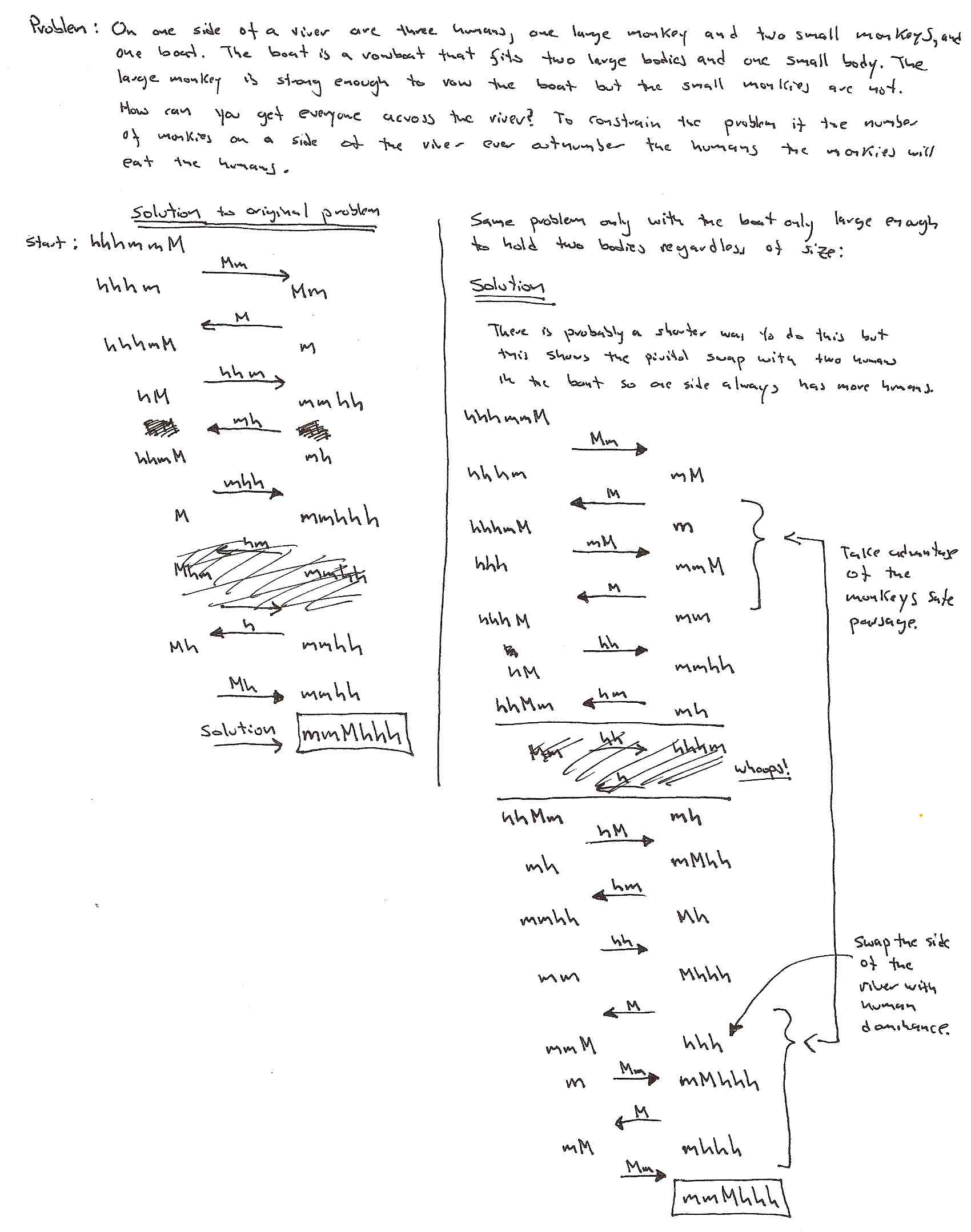
There is a room with a door (closed) and three light bulbs. Outside the room there are three switches, connected to the bulbs. You may manipulate the switches as you wish, but once you open the door you can’t change them. Identify each switch with its bulb.

Assumptions:

1. Assuming the lights are not the newer LED bulbs that dont get warm to the touch we can assume if we leave thei light on it will get warm.
2. We are powering up the box / it does not exsist before time T0. If not it is possible that the heating and cooling times will make the following simplification not work.

Two bulb Solution

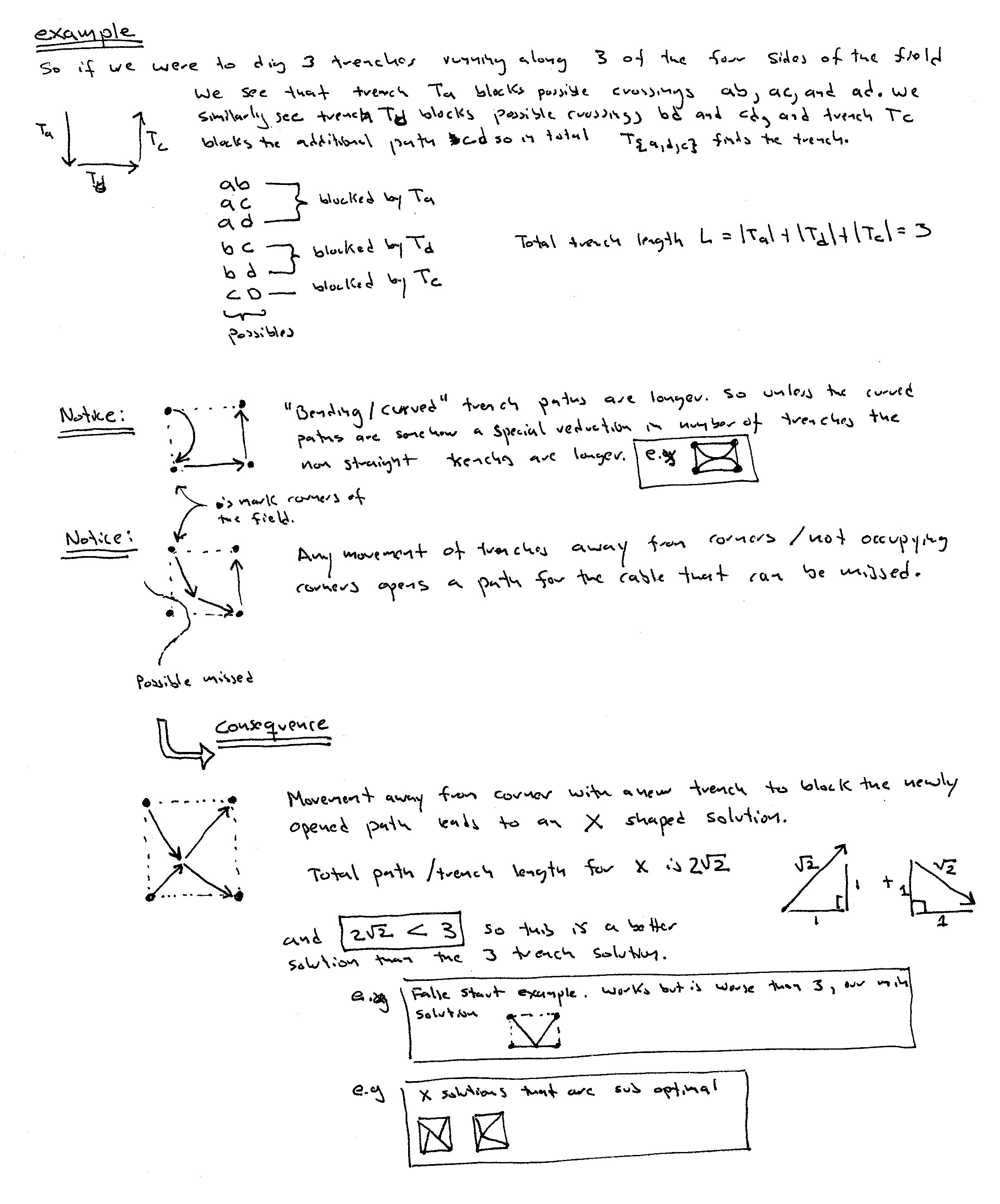
{S1 S2} = {a,b} –> Starting test state – wait for an hour.

{S1 !S2} = {a,!b} –> Toggle switch states and open the door.

1. Light that was constantly on should now be warm and on.
2. Light that was constantly off should still be off and cold.
3. Light that was on and is now off should be off and cold.
4. Light that was off and is now on shoudl be on and cold.

Tests 1 and 2 uniquely identify S1, and you get S2 by process of elimination.

Three bulb Solution

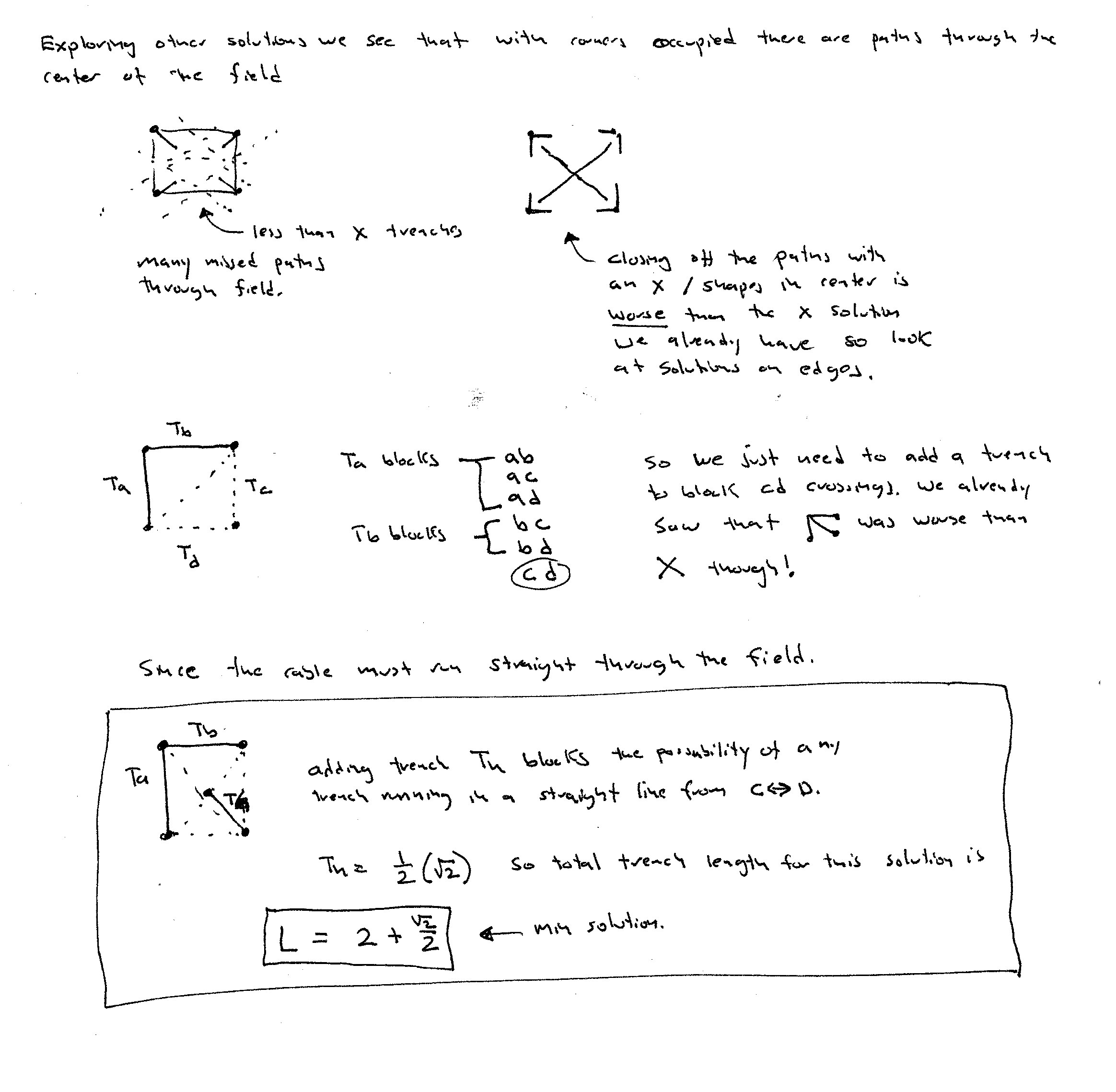
1. {S1  S2  S3} = {a,  b,   c} –> Starting test state – wait for X mins.
2. {S1  S2 !S3} = {a,  b, !c} –> Toggle switch and wait for Y mins.
3. {S1 !S2  S3} = {a,!b, c} –> Toggle switch and pen the door.

Decoding then is

1. S1. Light that was constantly on should either be ambient temperature and off or very hot and on.
2. S2. Should either be heated for X+Y mins and off, or ambient and on.
3. S3. Should either be heated for X-Y mins and on, or heated Y mins and off.

Four temperatures possible: Ambient, Y, X-Y, X+Y

1. Ambient and off light is S1.
2. Ambient and on light is S2.
3. Heated (X+Y) and on is S1.
4. heated (X+Y) and off it is S2.
5. Heated X-Y and on is S3 and heated Y and off is S3. So the medium temperature (either Y or X-Y)  is S3.

From 5 above we can collapse the temperature range to Ambient , {Y, X-Y}, X+Y. So just picking a X/Y ratio that allows for adaquade difference in heating and cooling times is all that is needed.

This is how the problem was phrased when I found it on the web.

You’ve got someone working for you for seven days and a gold bar to pay them. The gold bar is segmented into seven connected pieces. You must give them a piece of gold at the end of every day. If you are only allowed to make two breaks in the gold bar, how do you pay your worker?

Imagine an analog clock set to 12 o’clock. Note that the hour and minute hands overlap. How many times each day do both the hour and minute hands overlap? How would you determine the exact times of the day that this occurs? (Got this problem off of http://vijay.techi.googlepages.com/puzzles but it was one of their Microsoft questions).